汉字输入技术与应用研讨会论文集

论汉字的数学模型：九宫数码

戴顺天

序：用最简单的数学模型，准确的描述数以万计的形态复杂的汉字，是笔者18年来孜孜以求的奋斗目标。从1983年至1992年，用了九年的时间研制出两笔字型输入法，相关论文《论汉字的宏数学模型—太极码（两笔字型）汉字输入法》被录入1994年中文电脑国际学术会议大会论文集。从1993年至2002年，又用了第二个九年，研制出九宫写字板数码汉字输入法。本文将以九宫数码作为实施方案，探讨如何建立汉字的数学模型的问题。

在九宫数码研制过程中，得到了华绍和先生、胡金甫先生、柏松先生、何倩明女士、周刚民先生、胡文琬女士、肖哲仁先生、笔者夫人肖晓辉女士的无私帮助和支持，谨在此表示最衷心的感谢。

一、“点阵”与汉字

早期的汉字字库，几乎都是点阵汉字。从APPLEⅡ时代的9×9点阵到PC机时代的16×16点阵、24×24点阵等，都是用逐行逐点扫描的方法，罗列出每个点有无汉字笔画实体的信息，用一个二进制数字序列来描述一个汉字，并转换成十六进制代码储存。

显然，“点阵”方法的实质，是一种数学模型。它可以描述任何单色平面图形，“点阵”越大，描述越精确，但数据量也越庞大。

“点阵”用于由机器完成的汉字输出，无疑是可行的；用于由人进行的汉字输入，显然因其复杂性而不可取。

那么，“点阵”作为描述汉字的数学模型，使得它过于复杂的根本原因是什么呢？有没有简单一些的数学模型呢？有没有最简单的数学模型呢？

问题的症结在于：汉字并不是普通的平面图形。汉字具有一般的平面图形所没有的自身的规律性。所以，问题是可以大大简化的。

二、笔画与汉字

归根到底，汉字是由一个一个独立的笔画组成的。

只要建立起适合于任意一个笔画的数学模型，就可以把组成汉字的每一个笔画的数学模型简单的相加，成为任意一个汉字的数学模型。即：汉字 = 笔画1 + 笔画2 + 笔画3 +……+ 笔画n

由于每一个笔画都是完全独立的，所以，上述的数学表达式完全符合数学中加法的交换律。对于一个具体的汉字来说，就意味着与笔顺无关。事实上，汉字作为传达思想的工具，是通过它的字形，而与书写过程无关。

现在，所有的问题都归结到一点：对于一个完全独立的笔画，什么是全息的最简单的数学模型？

三、笔画与笔位

描述笔画的传统方法是编码，即人为的规定哪个数字代表哪种笔画。当然，这种方法并不是数学模型。例如：一撇一捺，可以组成汉字“人”，也可以组成汉字“入”，还可以组成汉字“八”。

仔细的审视“人”、“入”、“八”这三个汉字，可以得到三点结论：第一，它们的字形相近却又是确实不同的；第二，传统的形码编码方法不可能区分它们；第三，这三个汉字的区别在于笔画的位置。

事实上，数以万计的汉字都是由很少的几种笔形组成的，之所以会有万花筒似的纷繁复杂的千姿百态，笔画位置的差异是一个非常重要的原因。

传统编码方法所未能关注的，恰恰正是笔画的位置。

笔者认为，传统编码所最为关注的“笔形”、“笔顺”，仅仅是对笔画的小部分信息的描述。汉字“太”和“犬”，仅是末笔“点”的位置不同，就使得这两个汉字的字形字义迥异，更多的例子不胜枚举。这是“笔形”、“笔顺”所无法解决的问题。

本文特别提出“笔位”的概念，并以此作为研究和解决问题的出发点。

所谓笔位，是指一个独立笔画的全部实体在汉字中所处的位置。当然，笔位包含了笔画的起止、转折、长短、方位、笔形等全部信息，是对一个独立笔画的全息描述。

四、笔画的全息最简数学模型

汉字字形的最大特点是什么？是汉字大致呈方块形。

对笔画的深入研究使人想到笔位，方块汉字使人想到方块；笔位和方块使人想到九宫格子。

描述笔画位置，用一个格子显然是不行的；用2×2的四个格子呢？由于汉字字形的复杂性和笔画位置的多样性，显然难以较为确切的描述；用4×4的16 个格子或更多的n×n 个格子呢？那会导致太过复杂而且不能利用现有的数字小键盘；所以，笔者认为用3×3的九宫格子是最佳选择。它不仅可以较为确切的描述上下左右和四角，也能较为确切的描述上中下三部和左中右三部，中心部位（中宫）的存在为笔画的定位提供了极大的方便。特别重要的是，九宫恰好可以和现有的3×3通用数字小键盘相对应。我国传统文化认为最大的数字是九，这一点和阿拉伯数字最大是“9”相吻合。事实上，我们的祖先在很早以前就是用九宫来研究地理和方位的，并用九宫格子来练习汉字的书法。

现在用九宫格子来建立一个独立笔画的全息最简数学模型：

整个九宫的版面与方块汉字的版面相对应；每个九宫格小方块的宽度和高度是整个版面的三分之一，其面积是整个版面的九分之一，它绝不是仅仅一个点。给每个九宫格编上方位码1-9。方位码也就是笔位码，如下图所示。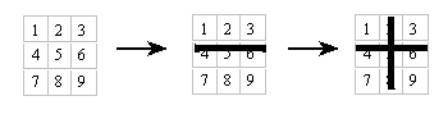

将方块汉字置入版面相同的九宫之中。因为任何笔画都在汉字的版面之内，所以任何笔画的全部实体都一定落在九宫之内，而且笔画的起点、转折点、终点都一定会落在某些九宫格之内。

所谓笔画，就是线段。折画可以看作是若干个直线段连结而成的折线。

一个独立笔画的全息最简数学模型是什么？

根据“两点决定一条直线”的数学公理，可以推知，一个直线段的全息最简数学模型，就是用直线段的两个端点的笔位码来描述。一个折线段的全息最简数学模型，就是用笔画的起点、转折点、终点的笔位码来描述。

从理论上说，笔画的起点和终点是可以互换的，和实际笔顺无关。例如：上图中的汉字“十”，横的笔位码是46或64，竖的笔位码是28或82。

实际上，必须引入笔顺规则：横的笔位码是46，竖的笔位码是28。

笔位码，就是一个独立笔画的全息最简数学模型。

五种基本笔形是横竖撇点折，其中的每一种，都有32种以上不同的笔位，“折”的笔位多达百余种。即一个笔画可以有两百多种不同的笔位。

五、汉字的全息最简数学模型和最佳实施方案

如前文所述，有了任意一个独立笔画的数学模型之后，只要把它们简单的相加，就可以得到相应汉字的数学模型了。

显然，一个汉字的所有笔画的全息最简数学模型的总和，就是整个汉字的全息最简数学模型。它提供一种几乎无重码的输入方法。

从理论上说，这种独立笔画相加为汉字的过程符合加法的交换律，可以是无序的，是和笔顺无关的。例如：上图中汉字“十”，可以是横加竖，也可以是竖加横，结果是完全相同的。

实际上，必须引入笔顺规则：汉字“十”等于横加竖。

以上是关于九宫数码的理论。

在实际进行汉字输入的时候，所谓汉字的全息最简数学模型，即按笔位输入汉字的全部笔画，显然并不是最佳实施方案。

笔者认为，最佳实施方案就是九宫数码输入法。

九宫数码输入法，定义数字小键盘的1-9九个数字键组成的方块是一个九宫写字板，每个数字键代表一个九宫格，数字就是笔位码，九宫格彼此之间是没有间隙的。这样，就可以利用数字小键盘模拟手写输入了。

由于笔位码是对笔画的全息描述，所以只要选择性的输入少量笔画，就可以使重码率较低，再辅以全范围单字高频先见和词组输入等措施，可以达到简易高效的目的。

由于是选择性的输入部分笔画，就有一个输入哪些笔画的问题；同时，必须完全遵循国家笔顺规范。为此，引入笔顺规则并严格遵守。

九宫数码提供了多种输入方式。最简单的方式是输入汉字的首笔和末笔。前文已经提到，一个笔画可以有两百多种不同的笔位，所以仅取首末两笔，理论上就有四万多组不同的编码；考虑到实际上首末笔笔位范围的约束，也有一万多组不同的编码，比之拼音仅有几百个音节，离散重码的能力已经远远超过了拼音输入。如果操作者愿意多输入一两个笔画，重码就更少了。

为了减少击键次数，允许引用金、木、水、火、土、日、月、人、女、口共十组特定部首；允许把折画的输入简化为只输入它的起点、第一个转折点、终点三个笔位码。

六、九宫数码输入法

如果请您在一张方格纸上写一个“十”字，您会怎么写呢？您一定会象下面的图示一样去写：

1-9九个数字键构成的方块,相当于一张方格纸,您完全可以同样的在上面“书写”方块汉字：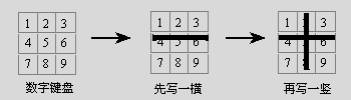

在数字键盘上“书写”汉字，比在纸上书写更加方便快捷。

例如：“书写”汉字“十”，先击打“横”的起点“4”和终点“6”，再击打“竖”的起点“2”和终点“8”就可以了。

这就是说，我们只要按照笔顺，击打笔画特殊点所在的九宫格“小方块”上的数字键，就可以方便的输入汉字。

为了轻松的在数字键盘上输入任何汉字，我们约定以下三点：

一、我们规定：输入笔画“折”，依次击打它的起始位置、转折位置、终止位置对应的数字键各1 次；输入“折”以外的其它笔画，只要击打它的起始位置、终止位置对应的数字键各1 次；输入“点” 或其它很短的笔画，在其对应位置击键2次；笔画终止位置有“钩”的，在终止位置增加击键1次；在笔画拥挤时，允许先输入的笔画被复盖。（其实只要完全理解了一个数字键是代表一个九宫格而不是仅一个点，九宫是3×3的格子，但绝不是3×3点阵，就永远没有“拥挤”和真正的“复盖”。）

二、输入汉字时，我们可以自由选择下述三种方式的任何一种，无须切换：

1、只输入汉字的首笔和末笔；例如：惠，对应13、99；

2、只输入汉字的首笔、第二笔、末笔；例如：惠，对应13、14、99；

3、具有明显的自然分割的合体字，先输入汉字第一个部件的首笔和末笔，再输入剩余部分的首笔和末笔；分不清部件的独体字，输入它的前三笔和末笔。

例如：惠，合体字，对应13、66、77、99；天，独体字，对应13、46、27、59；王，独体字，对应13、46、28、79。

三、为了减少击键次数，定义十组特定部件与数字一一对应：

例如：唱，对应06；明，对应67；如，对应90；妇，对应9、89。

如果您不想记这些部件，也可以使用只有一个部件“口”对应数字“0”的软件版本。

方便快捷的词组输入：二字词，输入每个字的首笔和末笔；例如：广州，对应数字键22、17、44、39；人口，对应数字键8、0；

三字词，输入每个字的首笔；例如：圣诞节，对应数字键134、11、13；

四字以上的词，输入前三末一个字的首笔；例如：全国人民代表大会，只取全、国、人、会四个字的首笔，对应数字键8、0、8、8；国家知识产权局，对应数字键0、22、24、136。

您还可以直接键入长途电话区号，方便的输入地名词组。例如：键入010，可以输入词组“北京”；键入020，可以输入词组“广州”。

七、结论

本文论述了汉字笔画的全息最简数学模型并提出了笔位的全新概念，在此基础上，提出了汉字全息最简数学模型的实施方案，即用数字小键盘模拟手写输入的九宫数码输入法。汉字笔画的全息最简数学模型是九宫数码的理论基础，九宫数码的成功是这一理论的佐证。

当然，所谓“全息”，也只是相对传统编码而言的，世界上本无任何绝对的东西。

九宫数码的编码依据，是笔画的笔位，是汉字本身所固有的特征，是一种自然存在的真实，因而也就是为人们所共知的。拼音输入为什么会有千百种输入法无可比肩的巨大的用户群？就是因为拼音是为许多人所共知的。共知性越大，就意味着学习难度越小，越容易上手。笔者认为，我国同胞有一种书写情结，可以常常见到有人在闲适时信手涂鸦。九宫数码具有比拼音更为广泛的共知基础，而且比拼音输入的重码低得多。与手写输入相比，九宫数码的优点也是显而易见的，它无须增加任何硬件，和手写输入一样直观，却比手写输入快捷得多。

九宫数码为全体华人提供了一种完全人性化的、极易上手的、方便快捷的汉字输入方法。从长远看，九宫数码必将拥有巨大的用户群，必将造福于社会。

可以自豪的说：九宫数码是一项重大的发明，是汉字输入技术发展的里程碑，是民族之瑰宝，是所有炎黄子孙的骄傲和光荣。九宫数码，必将与汉字同在。